Regression Problems

Regression is used to derive relationship between variables. If there are 2 variables then its called “Bi-Variant” data. If there are more than 2 variables, they are “Multi-Variant” data. By deriving this relationship, it will be used for predicting the value of one variable (Dependent variable) based on other variables (Independent variables).

Regression allows you to measure either influence of one or more variables on a dependent variable OR
Allows you to predict the value of a dependent variable based on the values of one or more dependent variable

Linear Regression

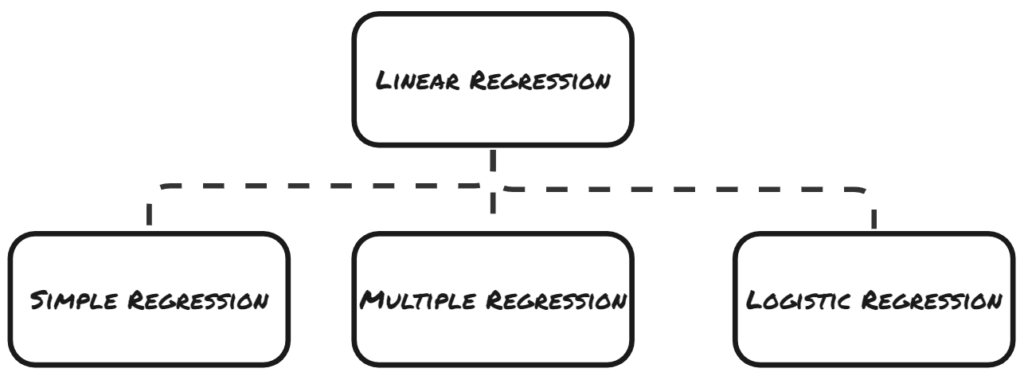
Both Simple and Multiple Linear Regression analysis is done when, the dependent variable is a metric (or continuous).

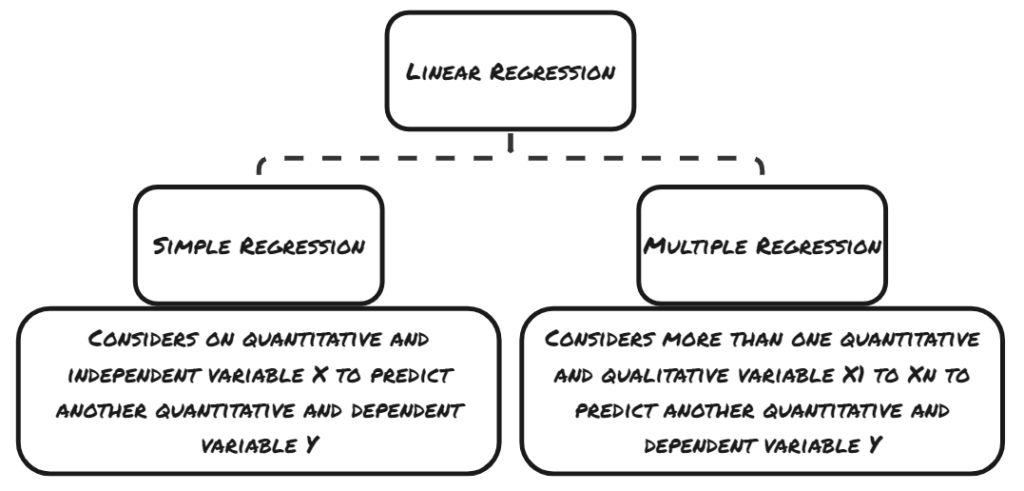
(a) Simple Linear Regression

In the simple linear regression, you have one dependent and one independent variable.
The basic form of regression is the linear regression.
It is in the form of Y = B₀ + B₁X + e, where ‘Y’ is the dependent variable and ‘X’ is the independent variable.
The relationship between the 2 variables can be plotted on a single line.
Examples of linear regression analysis include, predicting the house price vs house square-footage or between hours spent learning vs marks scored.

(b) Multiple Linear Regression

In multiple Linear Regression, you have single dependent variable, but multiple independent variable.

(c) Logistic Regression

logistic regression is a type of linear model.
Despite its name, logistic regression is used for binary classification problems, where the goal is to predict the probability that an instance belongs to a particular class (e.g., 0 or 1).
The logistic function (also called the sigmoid function) is used to map the linear combination of input features to a value between 0 and 1, representing the probability.

Logistic Regression is used when you have a categorical dependent variable. i.e. when you have yes or no answers you have logistic regression.
for example whether a person will buy the product or not?

Non-Linear Regression

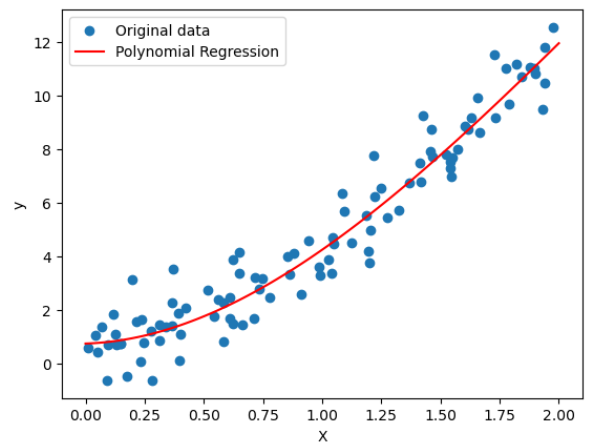
Polynomial Regression

Polynomial regression is a type of regression analysis in which the relationship between the independent variable (input) and the dependent variable (output) is modeled as an nth-degree polynomial. In other words, instead of fitting a linear equation to the data, as in simple linear regression, polynomial regression uses a polynomial equation of higher degree.
The general form of a polynomial regression equation is:

Sample Code

import numpy as np 
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
import matplotlib.pyplot as plt

# Generate some sample data
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 3 * X + 1.5 * X**2 + np.random.randn(100, 1)

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Transform the features to include polynomial terms up to degree 2
poly_features = PolynomialFeatures(degree=3, include_bias=False)
X_train_poly = poly_features.fit_transform(X_train)

# Fit a linear regression model to the polynomial features
poly_reg = LinearRegression()
poly_reg.fit(X_train_poly, y_train)

# Visualize the results
X_range = np.linspace(0, 2, 100).reshape(-1, 1)
X_range_poly = poly_features.transform(X_range)
y_range_pred = poly_reg.predict(X_range_poly)

plt.scatter(X, y, label='Original data')
plt.plot(X_range, y_range_pred, color='red', label='Polynomial Regression')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()

Classification Problems

In classification problems, the data is classified into 2 or more discrete categories. If it is into 2 categories, then it is called “Binary” or if it is into more than 2 then it is called “Multi-Class”.

#Machine Learning